SCIENCE 10
UNIT B: ENERGY FLOW IN TECHNOLOGICAL SYSTEMS
SCIENCE 10
Program of Studies
Unit B: Energy Flow in Technological Systems (Science and Technology Emphasis)
Overview: The first and second laws (conservation and conversion) of thermodynamics have been useful in the development of modern and efficient energy conversion devices. Students investigating mechanical energy conversions and transfers in systems will recognize that while energy is conserved, useful energy diminishes with each conversion. Students learn that energy can be observed only when it is being transferred, and that mechanical energy can be quantified. Energy conservation and conversion concepts are applied by students to explain energy conversions in natural and technological systems, and to investigate the design and function of energy conversion technologies.Links to Science
The following science concepts are related to the content of Unit B.Concepts
Science Course and Unit
- heat energy needs and technologies, thermal energy, heat transfer, energy conservation - Grade 7 Science, Unit C: Heat and Temperature
- forces on and within structures, direction of forces - Grade 7 Science, Unit D: Structures and Forces
- transmission of force and motion, simple machines, measurement of work in joules - Grade 8 Science, Unit D: Mechanical Systems
- forms of energy, energy transformation, renewable and nonrenewable energy - Grade 9 Science, Unit D: Electrical Principles and Technologies
- Which came first, science or technology, and is it possible for technological development to take place without help from pure science?
- How did efforts to improve the efficiency of heat engines result in the formulation of the first and second laws of thermodynamics?
- How can the analysis of moving objects help in the understanding of changes in kinetic energy, force and work?
- Why are efficiency and sustainability important considerations in designing energy conversion technologies?
Key Concepts
The following concepts are developed in this unit and may also be addressed in other units at other grade/course levels. The intended level and scope of treatment is defined by the outcomes below.- forms and interconversions of energy
- technological innovations of engines that led to the development of the concept of energy
- one-dimensional motion
- mechanical energy conversions and work
- design and function of technological systems and devices involving potential and kinetic energy and thermal energy conversions
- efficient use of energy, and the environmental impact of inefficient use of energy
Outcomes for Science, Technology and Society (STS) and Knowledge
Students will:- Analyze and illustrate how technologies based on thermodynamic principles were developed before the laws of thermodynamics were formulated
- illustrate, by use of examples from natural and technological systems, that energy exists in a variety of forms
(e.g., mechanical, chemical, thermal, nuclear, solar)
- describe, qualitatively, current and past technologies used to transform energy from one form to another, and that energy transfer technologies produce measurable changes in motion, shape or temperature
(e.g., hydroelectric and coal-burning generators, solar heating panels, windmills, fuel cells; describe examples of Aboriginal applications of thermodynamics in tool making, design of structures and heating)
- identify the processes of trial and error that led to the invention of the engine, and relate the principles of thermodynamics to the development of more efficient engine designs
(e.g., the work of James Watt; improved valve designs in car engines)
- analyze and illustrate how the concept of energy developed from observation of heat and mechanical devices
(e.g., the investigations of Rumford and Joule; the development of pre-contact First Nations and Inuit technologies based on an understanding of thermal energy and transfer)
- Explain and apply concepts used in theoretical and practical measures of energy in mechanical systems
- describe evidence for the presence of energy; i.e., observable physical and chemical changes, and changes in motion, shape or temperature
- define kinetic energy as energy due to motion, and define potential energy as energy due to relative position or condition
- describe chemical energy as a form of potential energy
(e.g., energy stored in glucose, adenosine triphosphate [ATP], gasoline)
- define, compare and contrast scalar and vector quantities
- describe displacement and velocity quantitatively
- define acceleration, quantitatively, as a change in velocity during a time interval: a = Δv/Δt
- explain that, in the absence of resistive forces, motion at constant speed requires no energy input
- recall, from previous studies, the operational definition for force as a push or a pull, and for work as energy expended when the speed of an object is increased, or when an object is moved against the influence of an opposing force
- define gravitational potential energy as the work against gravity
- relate gravitational potential energy to work done using Ep = mgh and W = Fd and show that a change in energy is equal to work done on a system: W = ΔE
- quantify kinetic energy using Ek = 1/2 mv2 and relate this concept to energy conservation in transformations
(e.g., for an object falling a distance “h” from rest: mgh = Fd = 1/2 mv2)
- derive the SI unit of energy and work, the joule, from fundamental units
- investigate and analyze one-dimensional scalar motion and work done on an object or system, using algebraic and graphical techniques
(e.g., the relationships among distance, time and velocity; determining the area under the line in a force–distance graph)
- Apply the principles of energy conservation and thermodynamics to investigate, describe and predict efficiency of energy transformation in technological systems
- describe, qualitatively and in terms of thermodynamic laws, the energy transformations occurring in devices and systems
(e.g., automobile, bicycle coming to a stop, thermal power plant, food chain, refrigerator, heat pump, permafrost storage pits for food)
- describe how the first and second laws of thermodynamics have changed our understanding of energy conversions
(e.g., why heat engines are not 100% efficient)
- define, operationally, “useful” energy from a technological perspective, and analyze the stages of “useful” energy transformations in technological systems
(e.g., hydroelectric dam)
- recognize that there are limits to the amount of “useful” energy that can be derived from the conversion of potential energy to other forms in a technological device
(e.g., when the potential energy of gasoline is converted to kinetic energy in an automobile engine, some is also converted to heat; when electrical energy is converted to light energy in a light bulb, some is also converted to heat)
- explain, quantitatively, efficiency as a measure of the “useful” work compared to the total energy put into an energy conversion process or device
- apply concepts related to efficiency of thermal energy conversion to analyze the design of a thermal device
(e.g., heat pump, high efficiency furnace, automobile engine)
- compare the energy content of fuels used in thermal power plants in Alberta, in terms of costs, benefits, efficiency and sustainability
- explain the need for efficient energy conversions to protect our environment and to make judicious use of natural resources
(e.g., advancement in energy efficiency; Aboriginal perspectives on taking care of natural resources)
Skill Outcomes
(focus on problem solving)Initiating and Planning
Students will:Ask questions about observed relationships, and plan investigations of questions, ideas, problems and issues
- design an experiment, identifying and controlling major variables
(e.g., design an experiment involving a combustion reaction to demonstrate the conversion of chemical potential energy to thermal energy)
- formulate operational definitions of major variables
(e.g., predict or hypothesize the conversion of energy from potential form to kinetic form, in an experiment using a pendulum or free fall)
Performing and Recording
Students will:Conduct investigations into relationships between and among observable variables, and use a broad range of tools and techniques to gather and record data and information
- carry out procedures, controlling the major variables and adapting or extending procedures
(e.g., perform an experiment to demonstrate the equivalency of work done on an object and the resulting kinetic energy; design a device that converts mechanical energy into thermal energy)
- compile and organize data, using appropriate formats and data treatments to facilitate interpretation of the data
(e.g., use a computer-based laboratory to compile and organize data from an experiment to demonstrate the equivalency of work done on an object and the resulting kinetic energy)
- use library and electronic research tools to collect information on a given topic
(e.g., compile information on the energy content of fuels used in Alberta power plants; trace the flow of energy from the Sun to the lighting system in the school, identifying what changes are taking place at each stage of the process)
- select and integrate information from various print and electronic sources or from several parts of the same source
(e.g., create electronic documents, containing multiple links, on using alternative energy sources, such as wind or solar, to generate electricity in Alberta; relate the importance of the development of effective and efficient engines to the time of the Industrial Revolution and to present-day first-world economics)
Analyzing and Interpreting
Students will:Analyze data and apply mathematical and conceptual models to develop and assess possible solutions
- compile and display evidence and information, by hand or using technology, in a variety of formats, including diagrams, flow charts, tables, graphs and scatterplots
(e.g.,plot distance–time, velocity–time and force–distance graphs; manipulate and present data through the selection of appropriate tools, such as scientific instrumentation, calculators, databases or spreadsheets)
- identify limitations of data or measurement
(e.g., recognize that the measure of the local value of gravity varies globally; use significant digits appropriately)
- interpret patterns and trends in data, and infer or calculate linear and nonlinear relationships among variables
(e.g., interpret a graph of changing kinetic and potential energy from a pendulum during one-half of a period of oscillation; calculate the slope of the line in a distance–time graph; analyze a simple velocity–time graph to describe acceleration; calculate the area under the line in a force–distance graph)
- compare theoretical and empirical values and account for discrepancies
(e.g., determine the efficiency of thermal energy conversion systems)
- state a conclusion based on experimental data, and explain how evidence gathered supports or refutes the initial hypothesis
(e.g., explain the discrepancy between the theoretical and actual efficiency of a thermal energy conversion system)
- construct and test a prototype of a device or system, and troubleshoot problems as they arise
(e.g., design and build an energy conversion device)
- propose alternative solutions to a given practical problem, identify the potential strengths and weaknesses of each and select one as the basis for a plan
(e.g., assess whether coal or natural gas should be used to fuel thermal power plants in Alberta)
- evaluate a personally designed and constructed device on the basis of self-developed criteria
(e.g., evaluate an energy conversion device based on a modern or traditional design)
Communication and Teamwork
Students will:Work as members of a team in addressing problems, and apply the skills and conventions of science in communicating information and ideas and in assessing results
- represent large and small numbers using appropriate scientific notation
- select and use appropriate numeric, symbolic, graphical and linguistic modes of representation to communicate ideas, plans and results
(e.g., use appropriate Système international (SI) units, fundamental and derived units; use advanced menu features within a word processor to accomplish a task and to insert tables, graphs, text and graphics)work cooperatively with team members to develop and carry out a plan and to troubleshoot problems as they arise(e.g., develop a plan to build an energy conversion device, seek feedback, test and review the plan, make revisions, and implement the plan)
Attitude Outcomes
Interest in ScienceStudents will be encouraged to:
Show interest in science-related questions and issues, and pursue personal interests and career possibilities within science-related fields
(e.g., apply concepts learned in the classroom to everyday phenomena related to energy; show interest in a broad scope of science-related fields in which energy plays a significant role)
Mutual Respect
Students will be encouraged to:
Appreciate that scientific understanding evolves from the interaction of ideas involving people with different views and backgrounds
(e.g., appreciate Aboriginal technologies of the past and present that use locally-available materials and apply scientific principles; recognize that science and technology develop in response to global concerns, as well as to local needs)
Scientific Inquiry
Students will be encouraged to:
Seek and apply evidence when evaluating alternative approaches to investigations, problems and issues
(e.g., assess problem using a variety of criteria; respect alternative solutions; honestly evaluate limitations of their designs; be persistent in finding the best possible answer or solution to a question or problem)
Collaboration
Students will be encouraged to:
Work collaboratively in carrying out investigations and in generating and evaluating ideas
(e.g., select a variety of strategies, such as group brainstorming, active listening, paraphrasing and questioning, to find the best possible solution to a problem; work as a team member when assigning and performing tasks; accept responsibility for problems that arise)
Stewardship Students will be encouraged to:
Demonstrate sensitivity and responsibility in pursuing a balance between the needs of humans and a sustainable environment
(e.g., recognize that their choices and actions, and the choices and actions that technologists make, can have an impact on others and on the environment)
Safety Students will be encouraged to:
Show concern for safety in planning, carrying out and reviewing activities
(e.g., demonstrate concern for self and others in planning and carrying out experimental activities and the design of devices; select safe methods for collecting evidence and solving problems)
Links to Mathematics The following mathematics outcomes are related to the content of Unit B but are not considered prerequisites.
- Data Collection and Analysis - Grade 9 Mathematics, Statistics and Probability (Data Analysis), Specific Outcome 3
- Measurement and Unit Conversions - Mathematics 10C, Measurement,Specific Outcomes 1 and 2; Mathematics 10-3, Measurement, Specific Outcome 1; Mathematics 20-3, Algebra, Specific Outcome 3; Mathematics 30-3, Measurement, Specific Outcome 1
- Rate and Proportions - Grade 8 Mathematics, Number, Specific Outcomes 3 and 4; Mathematics 20-2, Measurement, Specific Outcome 1
- Graph Analysis - Grade 9 Mathematics, Patterns and Relations (Patterns), Specific Outcome 2; Mathematics10C, Relations and Functions, Specific Outcomes 1 and 4; Mathematics 20-3, Statistics, Specific Outcome 1
- Solving Equations - Grade 9 Mathematics, Patterns and Relations (Variables and Equations), Specific Outcome 3; Grade 9 Mathematics, Number, Specific Outcome 6;
- Slope - Mathematics10C, Relations and Functions, Specific Outcome 3 and 5; Mathematics 20-3, Algebra, Specific Outcome 2
- Powers - Mathematics10C, Algebra and Number, Specific Outcome 3
- Scale Diagrams - Mathematics 20-2, Measurement, Specific Outcome 2; Mathematics 20-3, Geometry, Specific Outcome 2
Unit Focus Questions
- Which came first: science or technology, and is it possible for technological development to take place without help from “pure” science
- How did effort to improve the efficiency of heat engines result in the formation of the first and second laws of thermodynamics?
- How can the analysis of moving objects help in the understanding of changes in kinetic energy, force, and work?
- Why are efficiency and sustainability important considerations in designing energy conversion technologies?
Chapter B1.0 Investigating the energy flow in technological systems requires and understanding of motion, work, and energy
Key Concepts
- One-dimensional Motion
- Work
Learning Outcomes
- Define, compare and contrast scalar and vector quantities
- Describe displacement and velocity quantitatively
- Define acceleration quantitatively as a change in velocity during a time interval
- Explain that, in the absence of resistive forces, motion at constant speed requires no energy input.
- Recall from previous studies the operational definition for force as a push or pull, and work as energy expended when the speed of an object is increased or when an object is moved against the influence of an opposing force.
- Investigate and analyze one-dimensional scalar motion and work done on an object or system using algebraic and graphical techniques.
B1.1 Motion
Uniform Motion
Reference point – where you measure things from.Motion – the changing in position of an object relative to a reference point; an imaginary line joining the object to the reference point changes in length and direction or both.
How fast are you moving right now?
Most would answer you are stationary.
Some would say the world is spinning.
Some would say you are orbiting around the Sun.
Some would say the solar system is orbiting the centre of the galaxy.
All are correct, depending on where you measure zero from.
Most would answer you are stationary.
Some would say the world is spinning.
Some would say you are orbiting around the Sun.
Some would say the solar system is orbiting the centre of the galaxy.
All are correct, depending on where you measure zero from.
Uniform Motion – movement in a straight line at a constant speed. Does not speed up or slow down.
Non-uniform motion – movement that changes direction and/or changes speed.
Average Speed – the total distance traveled divided by the total time required to travel the distance
| v = | Δd |
→
→
|
| Δt |
- v - speed , m/s
- d - distance, m
- t - time, s
Ex. A person walks 500 m in 5 min. What was the person’s average speed?
v = d/t
v = 500 m / (5 min x 60 s/min)
v = 1.67 m/s
v = 500 m / (5 min x 60 s/min)
v = 1.67 m/s
| v = | Δd |
→
→
|
|
| Δt | |||
| v = | 500 m | ||
| (5 min x 60 s/min) | |||
| v = | 1.67 | m | |
| s | |||
d = vt
d = 15 m/s × 200 s
d = 3000 m
d = 3.0 × 103 m
d = 15 m/s × 200 s
d = 3000 m
d = 3.0 × 103 m
| Δ d = | v × Δ t |
→
→
|
||
| Δ d = | 15 | m | × 200 s | |
| s | ||||
| Δ d = | 3000 m | |||
| Δ d = | 3.0 × 103 m | |||
Ex. Convert 100 km/h into m/s.
100 km/h x 1000 m/ km x 1 h / 60 min x 1 min / 60 s = 27.8 m/s
To change km/h into m/s divide by 3.6
To change m/s into km/h multiply by 3.6
To change km/h into m/s divide by 3.6
To change m/s into km/h multiply by 3.6
| 100 | km | × | 1000 m | × | 1 h | × | 1 min | = 27.8 | m |
| h | 1 km | 60 min | 60 s | s | |||||
| 100 | km | × | 1000 m | × | 1 h | × | 1 min | = 27.8 | m |
| h | 1 km | 60 min | 60 s | s |
| Example Accelerations | |||
|---|---|---|---|
| 0.3 0 1 2 11 25 30 36 90 113 343 347 981 1 815 9 604 70 220 30 000 000 299 792 458 |
×10-9 .013 .0 .9 .95 |
m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s m/s |
Continental drift garden snail average walking speed 11.95 Usain Bolt in the 2009 Berlin World Championships 43 km/h peak speed of a galloping horse cheetah (fastest land animal) or sailfish (fastest fish) fastest human powered vehicle Canadian Sam Whittingham high speed train or diving peregrine Falcon (fastest bird) Bugatti Veyron SS (fastest production car) speed of sound Thrust SSC (fastest car) SR-71 Blackbird (fastest jet plane) X-15 (fastest manned rocket plane) X-43 scramjet (fastest plane) Space Shuttle speed of Helio 2 solar probe (fastest man mad object) speed of an electron in a cathode ray tube speed of light (3.00×108 m/s) speed limit of the universe (as far as we know) |
Practice Problems
Try practice problems 1 to 3 on page 128Using Graphs to Analyze Average Speed
Graphs are often used to represent the motion of a moving object.Graphs make it easy to interpret the motion.
The time is the manipulated variable.
The distance is the responding variable.
Slope is a mathematical measure of the steepness of the line on a graph.
It is a ratio of the rise (up) to the run (right).
On an graph the slope is the y-axis divided by the x-axis.
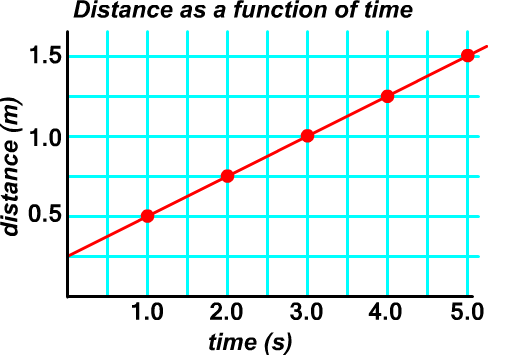
Ex. What is the slope of the graph?
Use points (1.0 s, 0.5 m) and (4.0, 1.25m)
v = Δd / Δt
v = (d2 - d1) / (t2 - t1)
v = (1.25 - 0.5 m) / (4.0 - 1.0 s)
v = 0.25 m/s
The velocity is 0.3 m/s. (rounded to one significant digit)
v = Δd / Δt
v = (d2 - d1) / (t2 - t1)
v = (1.25 - 0.5 m) / (4.0 - 1.0 s)
v = 0.25 m/s
The velocity is 0.3 m/s. (rounded to one significant digit)
| v = | Δd |
→
→
|
||
| Δt | ||||
| v = | Δd2 - Δd1 | |||
| Δt2 - Δt1 | ||||
| v = | 1.25 - 0.25 m | |||
| 4.0 - 1.0 s | ||||
| v = | 0.25 | m | ||
| s | ||||
The slope is easy to calculate for a perfect straight line graph. However, most experiments do not give a straight line graph. Linear regression gives the best possible slope.
You will see linear regression and slope in math 10 common.
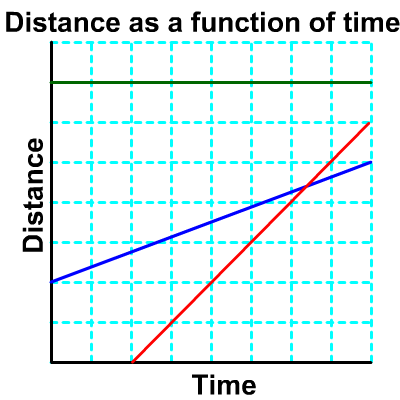
Which object (red, green or blue) is moving fastest?
- The red line is the fastest, because it has the steepest slope, is. it travels the most distance (vertical) in the lest time (horizontal).
- The blue line is the medium speed, because is has a less steep line.
- The green line is horizontal so its velocity (slope) is zero because it is not moving. It is stationary.
Practice Questions
Try practice problem 4 on page 130Toy Train Velocity Lab Interactive
Plotting a Speed-Time Graph
Time is the manipulated variable, X-axisSpeed is the responding variable, Y-axis
We have used d = vt .
On a speed vs time graph the v is the y axis and t is the x axis. If we multiple the v by t we get the area under the line.
Practice Questions
Try practice problem 5 on page 133B1.1 Motion Review
Review Questions
What is the equation for velocity?What is the difference between uniform and non uniform motion?
What is the manipulated variable on a distance vs time graph?
What is the responding variable on a distance vs time graph?
What is the manipulated variable on a speed vs time graph?
What is the responding variable on a speed vs time graph?
Practice Questions
B1.1 Check and Reflect page 135.
B1.2 Velocity
Scalar - quantity that indicates magnitude onlyEx. I walked 5.0 km
Vector – quantity that indicates magnitude and direction
Ex. I walked 5.0 km [North].
Distance Traveled and Displacement
Distance traveled – scalar quantity that measures how far an object has traveledDisplacement – vector quantity that measures the change in distance and the change in direction or position of an object
The navigator method
Used by navigators using a compass (boats, planes, orienteering). They used the north star as their reference point.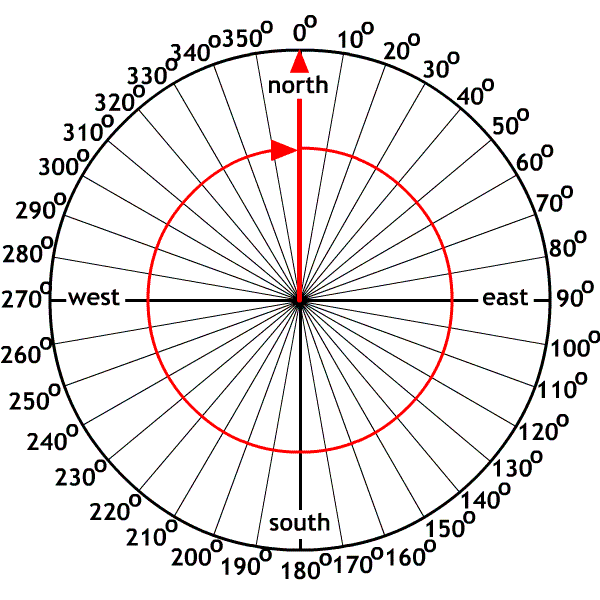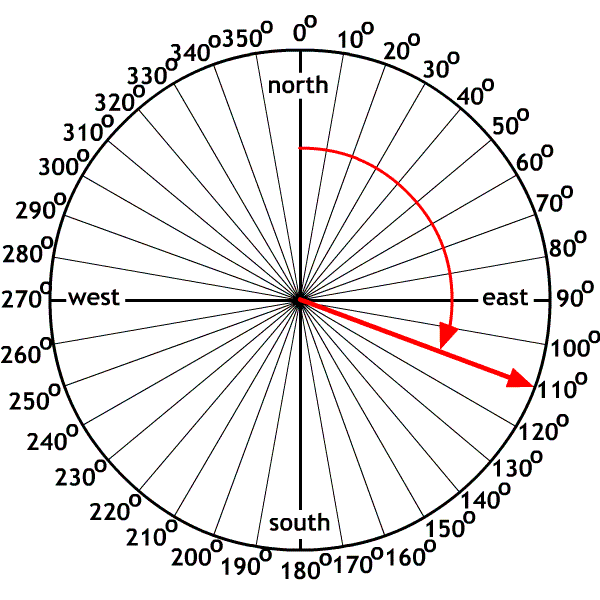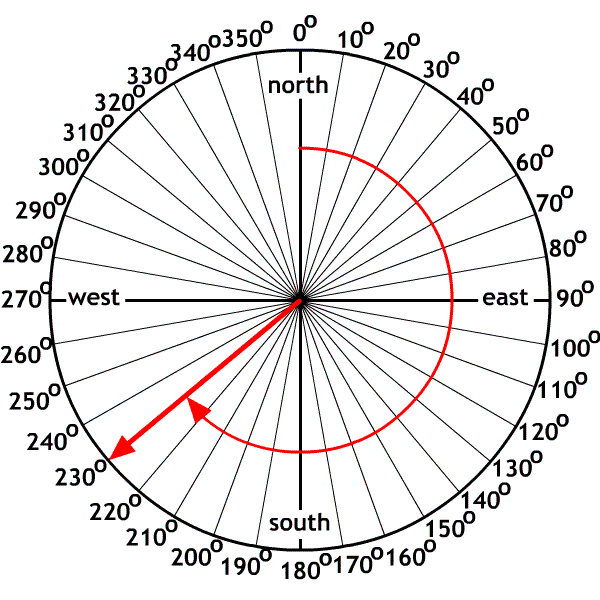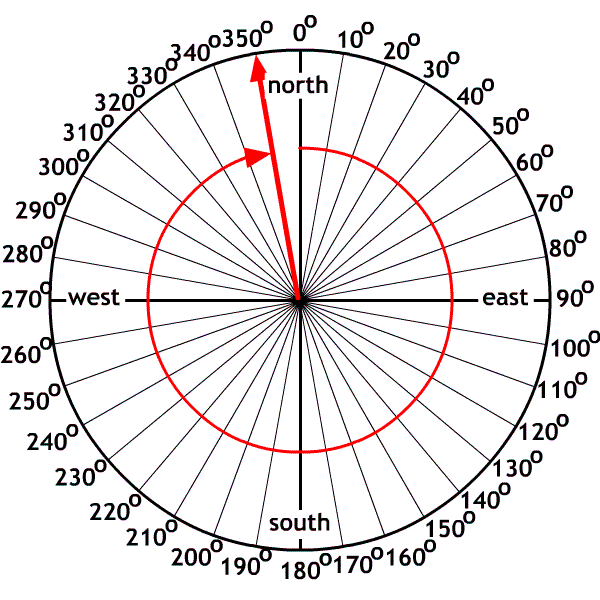
Ex. Draw the following vectors using the navigator method:
A. 60o
B. 200o
The X-axis, polar method
Used by mathematicians who started on the X-axis as zero degrees and rotated counter clockwise.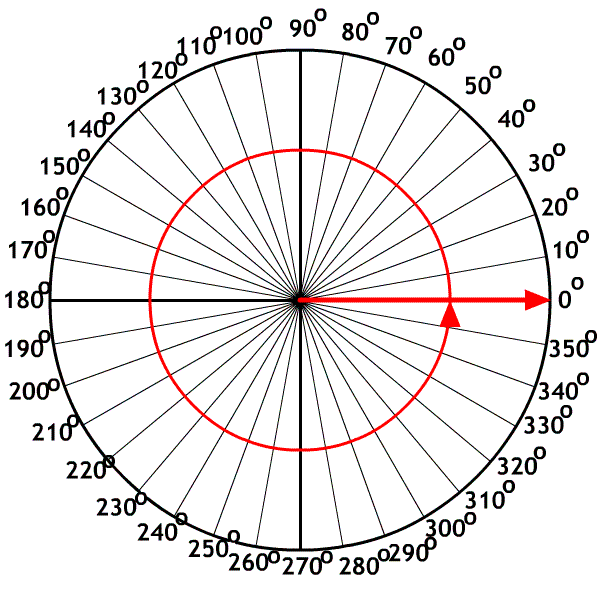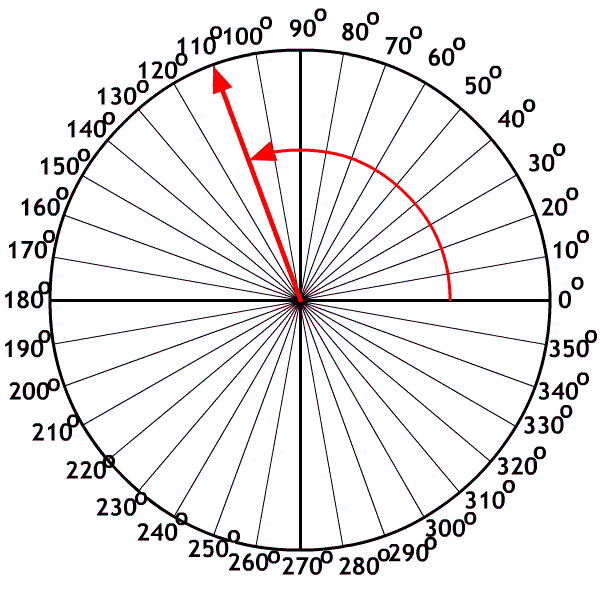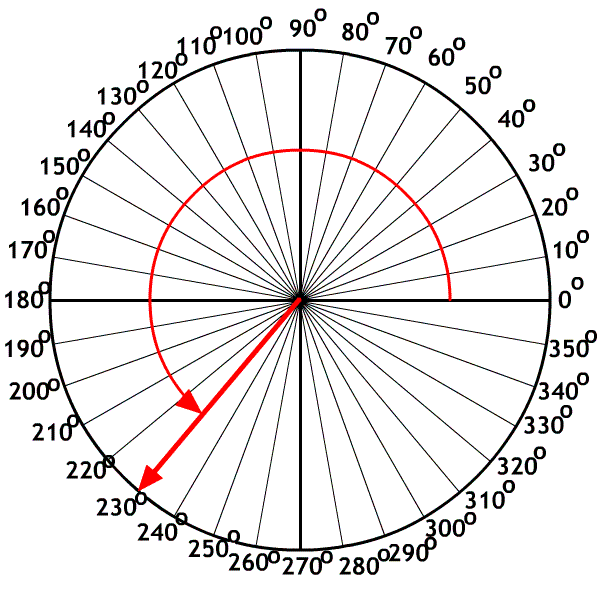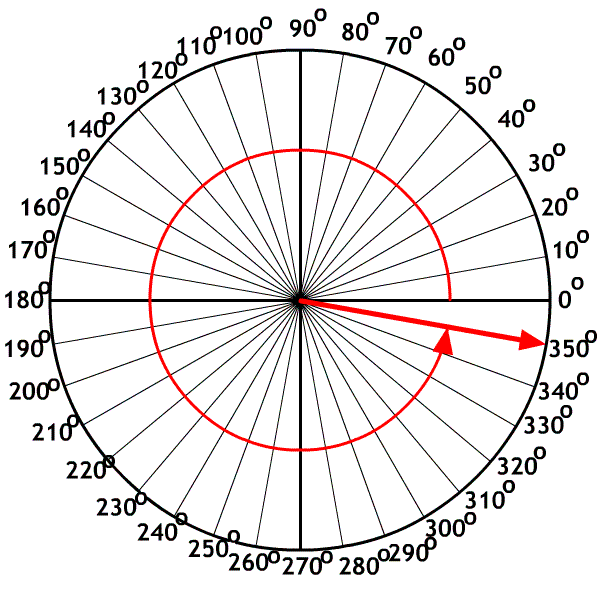
A. 40o
B. 160o
Practice Questions
Do practice problem 7 on page 140Practice Questions
Do practice Problem 6 on page 139.Ex. A dog runs 50 m [N] and then runs 25 m [S] in 75 seconds.
A. What is the dog’s average speed?
B. What is the dog’s average velocity?

Average Speed
average speed = distance travelled / elapsed time
v = Δd / Δt
v = (50 m + 25 m) / 75 s
v = 75 m / 75 s
v = 1.0 m/s
The average speed is 4.0 m/s.
v = Δd / Δt
v = (50 m + 25 m) / 75 s
v = 75 m / 75 s
v = 1.0 m/s
The average speed is 4.0 m/s.
| v = | Δd | |||
| Δt | ||||
| v = | 50 + 25 m | |||
| 75 s | ||||
| v = | 75 m | |||
| 75 s | ||||
| v = | 1.0 | m | ||
| s | ||||
average velocity = displacement / elapsed time
v = d / Δt
v = (50 m [N] + 25 m [S]) / 75 s
v = 25 m [N] / 75 s
v = 0.33 m/s [N] The average speed is 0.33 m/s [N].
The dog runs north and then south for 75 seconds or the owner can walk north at 0.33 m/s to meet the dog 25 m [N] 75 seconds later.
v = d / Δt
v = (50 m [N] + 25 m [S]) / 75 s
v = 25 m [N] / 75 s
v = 0.33 m/s [N] The average speed is 0.33 m/s [N].
The dog runs north and then south for 75 seconds or the owner can walk north at 0.33 m/s to meet the dog 25 m [N] 75 seconds later.
| v = | Δd |
→
→
|
|||
| Δt | |||||
| v = | 50 m [N] + 25 m [S] | ||||
| 75 s | |||||
| v = | 50 m [N] - 25 m [N] | ||||
| 75 s | |||||
| v = | 25 m [N] | ||||
| 75 s | |||||
| v = | 0.33 | m | [N] | ||
| s | |||||
B1.2 Velocity Review
Review Questions
Where is the zero angle for the navigator method?Where is the zero angle for the X-axis method?
What is the direction of rotation for the navigator method?
What is the direction of rotation for the X-axis method?
How can you identify a vector variable?
What does Δ mean?
Practice Questions
Do check and reflect on page 145.
B1.3 Acceleration
Types of Acceleration
Acceleration - change in velocity during a specific time interval| aave = | Δv |
→
→
|
| Δt |
| aave = | vf - vi |
→
→
→
|
| Δt |
- a - acceleration, m/s2
- v - velocity, m/s
- t - time, s
Positive acceleration is forward acceleration
Negative acceleration is backwards acceleration
Think of a car with no brakes, only forward and reverse gears.
What happens if you are driving forward and accelerate backwards?
What happens if you are driving backwards and accelerate forwards?
Practice Questions
Do practice problems 12-15 page 147Need graph of acceleration over time
Practice Questions
Do Practice Problem 16 page 149Acceleration Questions What acceleration can people survive?
What is a high acceleration?
What is a car’s acceleration?
| Example Accelerations | |||
|---|---|---|---|
| 0 1 1 2 2 3 3 4 4 8 10 9–12 46 60 80 106 |
.1654 .0 .55 .9 .5 .5 .3 .1 .2 .1 .1 .0 .2 |
g g g g g g g g g g g g g g g g |
Standing on the Moon at its equator (1/6 Earth) Standing on the Earth at sea level–standard Bugatti Veyron from 0 to 100 km/h in 2.4 s sneeze Gravitron amusement ride cough High-g roller coasters slap on back Top Fuel drag racing world record of 4.4 s over 1/4 mile hop off step plop down in chair Typical max. turn in an aerobatic plane or fighter jet Maximum for human on a rocket sled chest acceleration during car crash at 48 km/h with airbag, design limit limit of sustained human tolerance bullet in the barrel of a gun |
B1.3 Acceleration Review
Review Questions
What is the direction of positive acceleration?What is the direction of negative acceleration?
What is the manipulated variable on a speed vs. time graph?
What is the responding variable on a speed vs time graph?
.
B1.4 Work and Energy
Force
Force – any push or pull| a = | Fnet |
→
→
|
| m |
- F - force, N
- m - mass, kg
- a - acceleration, m/s2
Ex. A hare with a mass of 2.0 kg pushes with a force of 9.4 N. What is the hare's acceleration?
a = F / m
a = 9.4 N / 2.0 kg
a = 4.7 m/2
a = 9.4 N / 2.0 kg
a = 4.7 m/2
| a = | Fnet |
→
→
|
|
| m | |||
| a = | 9.4 N | ||
| 2.0 kg | |||
| a = | 4.7 | m | |
| s2 | |||
a = v / t
a = (28 - 0) m/s / 3.2 s
a = 8.75 m/s2
F = m a
F = 1443 kg x 8.75 m/s2
F = 1.26 x 104 N
a = (28 - 0) m/s / 3.2 s
a = 8.75 m/s2
F = m a
F = 1443 kg x 8.75 m/s2
F = 1.26 x 104 N
| a = | Δv |
→
→
|
|
| Δt | |||
| a = | 28 - 0 m/s | ||
| 3.2 s | |||
| a = | 8.75 | m | |
| s2 | |||
| F = | m × a |
→
→
|
|||
| F = | 1443 kg × 8.75 | m | |||
| s2 | |||||
| F = | 8.75 | m | |||
| s2 | |||||
A Newton is not a base SI unit, it is made up of kg, m and seconds.
1 N = 1 kg x m / s2
We use the Newton because it is easier and more convenient.
Force Questions
Work
Work – the energy transferred from one object to another.→
→
- W - work, J
- F - Force, N
- d - distance, m
- There must be movement
- There must be a force
- The force and the displacement must be in the same direction
Ex. A gardener pushes a wheelbarrow with 800 N [west] as distance of 20 m [west]. How much work did the gardener do?
W = F x d →
→
W = 800 m [west] x 20 m [west]
W = 16 000 J
W = 1.6 x 104 J
W = 800 m [west] x 20 m [west]
W = 16 000 J
W = 1.6 x 104 J
Ex. An airplane with a mass of 50 tonnes uses 6.0 x 108 J accelerate over a distance 1.5 km. What is the plane's acceleration?
F = W /d
F = 6.6 x 108 J / 1.5 x 103 m
F = 440 000 N
a = F/m
a = 440 000 N / 50 x 103 kg
a = 8.8 m/s2
F = 6.6 x 108 J / 1.5 x 103 m
F = 440 000 N
a = F/m
a = 440 000 N / 50 x 103 kg
a = 8.8 m/s2
| F = | W |
→
→
|
||
| d | ||||
| F = | 6.6 × 108 J | |||
| 1.5 × 103 m | ||||
| F = | 400 000 N | |||
| a = | F |
→
→
|
|
| m | |||
| a = | 440 000 N | ||
| 50 × 103 kg | |||
| a = | 8.75 | m | |
| s2 | |||
Practice Questions
Do Practice Problems 18 to 20 page 160Energy
Energy – the ability to do workNote that the definition of work uses energy and the definition of energy uses work. The definitions are circular. It is almost impossible to describe work and energy without examples.
Work Questions
B1.4 Work and Energy Review
Review Questions
What is a force?What is work?
What are the units for force?
What are the units for work?
Practice Questions
Unit B1.0 Section ReviewLinear Regression Example

