PHYSICS 20
Unit 1: Kinematics
Unit Themes and Emphases
Change and SystemsFocusing Questions
- How do changes in position, velocity, and acceleration allow us to predict the paths of moving objects and systems?
- How do the principles of kinematics influence the development of new mechanical technologies?
Unit A: Kinematics
Themes: Change and SystemsOverview: In this unit, students investigate changes in the position and velocity of objects and systems in a study of kinematics.
This unit builds on:
- Grade 7 Science, Unit D: Structures and Forces
- Grade 8 Science, Unit D: Mechanical Systems
- Science 10, Unit B: Energy Flow in Technological Systems
Unit A will require approximately 15% of the time allotted for Physics 20.
Links to Mathematics: Refer to page 20.
Focusing Questions:
- How do changes in position, velocity and acceleration allow us to predict the paths of moving objects and systems?
- How do the principles of kinematics influence the development of new mechanical technologies?
There is one major outcome in this unit.
Students will:
A1. describe motion in terms of displacement, velocity, acceleration and time.
Key Concepts: The following concepts are developed in this unit and may also be addressed in other units or in other courses. The intended level and scope of treatment is defined by the outcomes.
- scalar quantities
- vector quantities
- uniform motion
- uniformly accelerated motion
- two-dimensional motion
General Outcome A1. students will describe motion in terms of displacement, velocity, acceleration and time.
Specific Outcomes for KnowledgeStudents will:
20–A1.1k define, qualitatively and quantitatively, displacement, velocity and acceleration
20–A1.2k define, operationally, and compare and contrast scalar and vector quantities
20–A1.3k explain, qualitatively and quantitatively, uniform and uniformly accelerated motion when provided with written descriptions and numerical and graphical data
20–A1.4k interpret, quantitatively, the motion of one object relative to another, using displacement and velocity vectors
20–A1.5k explain, quantitatively, two-dimensional motion in a horizontal or vertical plane, using vector components.
Specific Outcomes for Science, Technology and Society (STS) (Nature of Science Emphasis)
Students will:
20–A1.1sts explain that the goal of science is knowledge about the natural world (NS1)
- identify common applications of kinematics, such as determining the average speed of a run, bike ride or car trip, or the acceleration required to launch an aircraft from a carrier
20–A1.2sts explain that scientific knowledge is subject to change as new evidence becomes apparent and as laws and theories are tested and subsequently revised, reinforced or rejected (NS4)
- analyze lunar free fall as illustrated in a video
20–A1.3sts explain that the process for technological development includes testing and evaluating designs and prototypes on the basis of established criteria (ST5d) [ICT C6–4.5]
- investigate the application of kinematics principles, such as determining the appropriate length of airport runways, the design of merging lanes or the timing of traffic lights
Specific Outcomes for Skills (Nature of Science Emphasis)
Initiating and Planning
Students will:
20–A1.1s formulate questions about observed relationships and plan investigations of questions, ideas, problems and issues
- identify, define and delimit questions to investigate; e.g., What are the relationships among displacement, velocity, acceleration and time? (IP–NS1)
- explain why distances are measured in different units (as the crow flies, days of travel, mileage from city centre to city centre, light years).
Performing and Recording
Students will:
20–A1.2s conduct investigations into relationships among observable variables and use a broad range of tools and techniques to gather and record data and information
- perform an experiment to demonstrate the relationships among displacement, velocity, acceleration and time, using available technologies; e.g., interval timers, photo gates (PR–NS2, PR–NS3) [ICT C6–4.4]
- collect information from various print and electronic sources to explain the use of kinematics concepts; e.g., the synchronization of traffic lights (PR–ST1) [ICT C1–4.1].
Analyzing and Interpreting
Students will:
20–A1.3s analyze data and apply mathematical and conceptual models to develop and assess possible solutions
- construct graphs to demonstrate the relationships among displacement, velocity, acceleration and time for uniform and uniformly accelerated motion (AI–NS2)
- analyze a graph of empirical data to infer the mathematical relationships among displacement, velocity, acceleration and time for uniform and uniformly accelerated motion (AI–NS2) [ICT C7–4.2]
- solve, quantitatively, projectile motion problems near Earth’s surface, ignoring air resistance (AI–NS3)[ICT C6–4.1]
- relate acceleration to the slope of and displacement to the area under, a velocity-time graph (AI–NS2, AI–NS6) [ICT C7–4.2]
- analyze uniform motion examples, using computer simulations (AI–NS3) [ICT C6–4.4].
Communication and Teamwork
Students will:
20–A1.4s work collaboratively in addressing problems and apply the skills and conventions of science in communicating information and ideas and in assessing results
- use appropriate Système international(SI) units, fundamental and derived units and significant digits (CT–NS2)
- use appropriate numeric, symbolic, graphical and linguistic modes of representation to communicate ideas, plans and results (CT–NS2)
- use delta notation correctly when describing changes in quantities (CT–NS2).
To be developed throughout the course.
Links to Mathematics
The following mathematics outcomes are related to the content of Unit A but are not considered prerequisites.
Concept - Mathematics Course, Strand and Specific Outcome
Data Collection and Analysis
- Grade 9 Mathematics, Statistics and Probability (Data Analysis),Specific Outcome 3
- Mathematics 10C,Measurement,Specific Outcomes 1 and 2;
- Mathematics 10-3, Measurement, Specific Outcome 1;
- Mathematics 20-3, Algebra, Specific Outcome 3
- Mathematics 10C, Measurement, Specific Outcome 4;
- Mathematics 10-3, Geometry, Specific Outcomes 2 and 4
- Mathematics 20-2,Measurement,Specific Outcome 1
- Mathematics10C, Relations and Functions,Specific Outcomes 1, 4 and 7;
- Mathematics 20-3, Statistics,Specific Outcome 1 Solving Equations
- Grade 9 Mathematics, Number, Specific Outcome 6
- Mathematics 20-2,Measurement,Specific Outcome 2;
- Mathematics 20-3, Geometry, Specific Outcome 2
- Mathematics10C, Relations and Functions,Specific Outcomes3 and 5;
- Mathematics 20-3, Algebra, Specific Outcome 2 Area Calculations
- Mathematics 10-3, Measurement, Specific Outcome 4
- Mathematics10C, Algebra and Number, Specific Outcome 3
Chapter 2: Vector Components Describe Motion in Two Dimensions
Key Concepts
- two-dimensioal motion
- vector methods
Knowledge
- Explain two-dimensional motion in a horizontal or vertical plane.
- Interpret the motion of one object relative to another.
STS
- Explain that scientific knowledge is subject to change as new evidence comes to light and as laws and theories are tested, restricted, revised or reinforced.
2.1 Vector Methods In One Dimension
Collinear – along the same straight line, either in the same or in opposite directions.Resultant vector – a vector drawn from the tail of the first vector to the tip of the last vector.
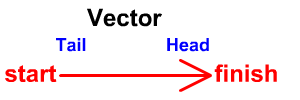
How are added vectors drawn?
They are drawn tail to head, tail to head.
What is the resultant vector?
The resultant is the sum of the vectors.
Practice Problems # 1 p.73
Practice Problems #1-3 p. 74
2.1 Check and Reflect p. 75
Knowledge # 1-4
Applications # 5-9
2.2 Motion in Two Dimensions
All diagonals can be broken into components (X and Y parts)The X and Y components define the resultant diagonal vector.
There a two methods used to describe directions.
Ex. A sailor leaves port and travels 5.0 km east and then 9.0 km north. What is the boat’s displacement?
Adding Vectors
Draw a diagram
Determine the X and Y components
Add the X components
Add the Y components
Reassemble the X and Y components into the resultant.
Ex. A bird flies 5.0 km [NW] and then flies 3.0 km [70owouth of west]. What is the bird’s displacement?
Review Questions
Describe the Cartesian (mathematical, polar) method of vectors.Describe the navigator method of vectors
How do you determine the x-components of a vector?
How do you determine the y-components of a vector?
Check and Reflect p. 90
Knowledge # 1-3
Applications # 4-11
2.3 Relative Motion
Relative motion – motion measured with respect to an observer.Ex. A canoeist paddling 1.5 m/s north is going across a river flowing 2.5 m/s west.
a. What is the velocity of the canoeist relative to the shore?
Ex. A canoeist paddling 3.5 m/s is going across a river flowing 2.5 m/s west. What direction does the canoeist have to paddle to go straight across the river?
Police car Chase
When the frame of reference is parallel to the motion.
Crossing a River
When the frame of reference is perpendicular to the motion.
P. 101
Knowledge 1-4
Applications 5-11
Review Questions
What is relative motion?Why do we use relative motion?
2.4 Projectile Motion
Trajectory – the parabolic path of a projectile.Break the initial velocity into X and Y components.
Use the Y components to solve for time
Use the X components to solve for the range (horizontal velocity)
Projectile Motion Simulation
Ex. A ball is hit at 30 m/s at an angle of 60o. How far away will it land?
Ex. A ball is hit at 30 m/s at an angle of 30o. How far away will it land?
(keep the 60o graph)
What do you notice about where each lands?
What is the pattern about angles and distance?
What angle gives the best distance?
45o is the best combination of height and distance to get the best distance.
Review Questions
When does projectile motion apply?What determines the time of flight?
What equation is used to calculate the time of flight?
What equation is used to calculate the range?

