PHYSICS 20
Unit 4: Oscillatory Motion and Mechanical Waves
Unit Themes and Emphases
- Change, Energy and Matter
- Scientific Inquiry
- Nature of Science
Focusing Questions
- Where do we observe oscillatory motion?
- How do mechanical waves transmit energy?
- How can an understanding of the natural world improve how society, technology and the environment interact?
Unit D: Oscillatory Motion and Mechanical Waves
Themes: Energy and Matter
Overview:
In this unit, students investigate simple harmonic motion and mechanical waves.This unit builds on:
- Science 10, Unit B: Energy Flow in Technological Systems
- Physics 20, Unit A: Kinematics; Unit B: Dynamics; and Unit C: Circular Motion, Work and Energy
Unit D will require approximately 30% of the time allotted for Physics 20.
Focusing Questions:
- What are examples of oscillatory motion in the world around us?
- How do mechanical waves transmit energy?
- How is structural design and the development of technologies influenced by our understanding of wave properties?
General Outcomes:
There are two major outcomes in this unit.Students will:
D1. describe the conditions that produce oscillatory motion
D2. describe the properties of mechanical waves and explain how mechanical waves transmit energy.
Key Concepts:
The following concepts are developed in this unit and may also be addressed in other units or in other courses. The intended level and scope of treatment is defined by the outcomes.- oscillatory motion
- simple harmonic motion
- restoring force
- oscillating spring, pendulum
- mechanical resonance
- mechanical waves—longitudinal and transverse
- universal wave equation
- reflection
- interference
- acoustic resonance
- Doppler effect
General Outcome 1
1. describe the conditions that produce oscillatory motionSpecific Outcomes for Knowledge
Students will:
20–D1.1k describe oscillatory motion in terms of period and frequency
20–D1.2k define simple harmonic motion as a motion due to a restoring force that is directly proportional and opposite to the displacement from an equilibrium position
20–D1.3k explain, quantitatively, the relationships among displacement, acceleration, velocity and time for simple harmonic motion, as illustrated by a frictionless, horizontal mass-spring system or a pendulum, using the small-angle approximation
20–D1.4k determine, quantitatively, the relationships among kinetic, gravitational potential and total mechanical energies of a mass executing simple harmonic motion
20–D1.5k define mechanical resonance.
20–D1.2k define simple harmonic motion as a motion due to a restoring force that is directly proportional and opposite to the displacement from an equilibrium position
20–D1.3k explain, quantitatively, the relationships among displacement, acceleration, velocity and time for simple harmonic motion, as illustrated by a frictionless, horizontal mass-spring system or a pendulum, using the small-angle approximation
20–D1.4k determine, quantitatively, the relationships among kinetic, gravitational potential and total mechanical energies of a mass executing simple harmonic motion
20–D1.5k define mechanical resonance.
Specific Outcomes for Science, Technology and Society (STS) (Nature of Science Emphasis)
Students will:
20–D1.1sts explain that the goal of science is knowledge about the natural world (NS1)
• analyze, qualitatively, the forces in real-life examples of simple harmonic motion:
- action of springs in vehicle suspensions
- mechanical resonance in cars, bridges and buildings
- seismic waves in Earth’s crust
• relate the fundamental frequency and amplitude of a vibrating drum membrane to its properties.
Note: Some of the outcomes are supported by examples. The examples are written in italics and do not form part of the required program but are provided as an illustration of how the outcomes might be developed.
• analyze, qualitatively, the forces in real-life examples of simple harmonic motion:
- action of springs in vehicle suspensions
- mechanical resonance in cars, bridges and buildings
- seismic waves in Earth’s crust
• relate the fundamental frequency and amplitude of a vibrating drum membrane to its properties.
Note: Some of the outcomes are supported by examples. The examples are written in italics and do not form part of the required program but are provided as an illustration of how the outcomes might be developed.
Specific Outcomes for Skills (Nature of Science Emphasis)
Initiating and PlanningStudents will:
20–D1.1s formulate questions about observed relationships and plan investigations of questions, ideas, problems and issues
• design an experiment to demonstrate that simple harmonic motion can be observed within certain limits, relating the frequency and period of the motion to the physical characteristics of the system;
e.g., a frictionless horizontal mass-spring system or a pendulum (IP–NS2)
• predict the conditions required for mechanical resonance (IP–NS3).
• design an experiment to demonstrate that simple harmonic motion can be observed within certain limits, relating the frequency and period of the motion to the physical characteristics of the system;
e.g., a frictionless horizontal mass-spring system or a pendulum (IP–NS2)
• predict the conditions required for mechanical resonance (IP–NS3).
Performing and Recording
Students will:
20–D1.2s conduct investigations into relationships among observable variables and use a broad range of tools and techniques to gather and record data and information
• perform an experiment to determine the relationship between the length of a pendulum and its period of oscillation (PR–NS3)
• perform an experiment to illustrate the phenomenon of mechanical resonance (PR–NS3)
• perform an experiment to determine the spring constant of a spring (PR–NS3).
• perform an experiment to determine the relationship between the length of a pendulum and its period of oscillation (PR–NS3)
• perform an experiment to illustrate the phenomenon of mechanical resonance (PR–NS3)
• perform an experiment to determine the spring constant of a spring (PR–NS3).
Analyzing and Interpreting
Students will:
20–D1.3s analyze data and apply mathematical and conceptual models to develop and assess possible solutions
• relate the length of a pendulum to its period of oscillation (AI–NS2) [ICT C7–4.2]
• ask if the mass of the pendulum bob is a factor in the pendulum’s period of oscillation (AI–NS5).
• relate the length of a pendulum to its period of oscillation (AI–NS2) [ICT C7–4.2]
• ask if the mass of the pendulum bob is a factor in the pendulum’s period of oscillation (AI–NS5).
Communication and Teamwork
Students will:
20–D1.4s work collaboratively in addressing problems and apply the skills and conventions of science in communicating information and ideas and in assessing results
• select and use appropriate numeric, symbolic, graphical or linguistic modes of representation to communicate findings and conclusions (CT–NS2).
Note: Some of the outcomes are supported by examples. The examples are written in italics and do not form part of the required program but are provided as an illustration of how the outcomes might be developed. • select and use appropriate numeric, symbolic, graphical or linguistic modes of representation to communicate findings and conclusions (CT–NS2).
Links to Mathematics
The following mathematics outcomes are related to the content of Unit D but are not considered prerequisites.Concept - Mathematics Course, Strand and Specific Outcome
Data Collection and Analysis
Grade 9 Mathematics, Statistics and Probability (Data Analysis), Specific Outcome 3
Measurement andUnit Conversions
Mathematics 10C, Measurement, Specific Outcomes 1 and 2;
Mathematics 10-3, Measurement, Specific Outcome 1;
Mathematics 20-3, Algebra, Specific Outcome 3
Trigonometry
Mathematics 10C, Measurement, Specific Outcome 4;
Mathematics 10-3, Geometry, Specific Outcomes 2 and 4
Rate and Proportions
Mathematics 20-2, Measurement, Specific Outcome 1
Graph Analysis
Mathematics10C, Relations and Functions, Specific Outcomes 1, 4 and 7;
Mathematics 20-3, Statistics, Specific Outcome 1
Mathematics 30-1, Trigonometry, Specific Outcome 4
Mathematics 30-2, Relations and Functions, Outcome 8
Solving Equations
Grade 9 Mathematics, Number, Specific Outcome 6;
Mathematics 20-2, Number and Logic, Specific Outcome 4;
Mathematics 20-1, Algebra and Number, Specific Outcomes 3 and 6;
Mathematics 30-2, Relations and Functions, Specific Outcome 3
Slope
Mathematics10C, Relations and Functions, Specific Outcomes 3 and 5;
Mathematics 20-3, Algebra, Specific Outcome 2
Powers
Mathematics10C, Algebra and Number, Specific Outcome 3
Note: The use of systems of equations, the quadratic formula and trigonometric ratios for angles greater than 90º is not required in this unit.
Chapter 7: Oscillatory motion requires a set of conditions
Unit Themes and Emphases
- Oscillatory motion
- Simple harmonic motion
- Restoring force
- Oscillating spring and pendulum
- Mechanical resonance
Learning Outcomes
- Describe oscillatory motion in terms of period and frequency
- Define simple harmonic motion as being due to a restoring force that is directly proportional and opposite to the displacement of an object from an equilibrium position.
- Explain the quantitative relationships among displacement, acceleration, velocity, and time for simple harmonic motion.
- Define mechanical resonance.
STS
- Explain that the goal of science is knowledge about the natural world.
7.1 Period and Frequency
Period (T) - is the time for one complete cycle, measured in seconds (s). If the period of each cycle remains constant, the object is moving with oscillatory motion.Frequency (f) - is the number of cycles per second measured in Hertz (Hz).
| T = | 1 |
| f |
f - frequency, Hz or 1/s or s-1
Oscillation – one period or complete motion of repeating motion.
Cycle – see oscillation.
Oscillatory motion – motion in which the period of each cycle is constant
7.2 Simple Harmonic Motion
Simple harmonic motion – oscillatory motion where the restoring force is proportional to the displacement of the massRestoring force – a force acting opposite to the displacement to move the object back to its equilibrium position
The pendulum is a simple harmonic oscillator for angles less than 15o.
A pendulum’s period is determined by its length and the acceleration of gravity, but not the mass of the bob.
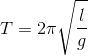
| T = 2 π √ | l |
| g |
l - length, m
g - acceleration due to gravity, 9.81 m/s2 on Earth
What is the period of a 20 cm pendulum?
How do you adjust the time of a pendulum clock?
7.3 Position, Velocity, Acceleration, and Time Relationships
When does a pendulum move slowest?When does a pendulum move fastest?
When is the restoring force the largest?
When is the restoring force the smallest?
When is the acceleration the largest?
When is the acceleration the smallest?
Resonant frequency – the natural frequency of vibration of an object.
Amplitude – how far the mass moves from equilibrium.
Mechanical resonance – the increase in amplitude of oscillation of a system as a result of a periodic force whose frequency is equal or very close to the resonant frequency of the system
Small force at the resonant frequency = large amplitude
Bridges and buildings can resonate due to the force of the wind.
Program of Studies
Alberta Physics 20
Program of Studies
Alberta Physics 20
Program of Studies
Contact me:
BCHS Barrhead AB
Steven Montgomery
steven.montgomery@pembinahills.caBCHS Barrhead AB
Textbook
Physics 20 & 20 Textbook (2009)
Physics 20 & 20 Textbook (2009)