PHYSICS 20
Unit 3: Circular Motion, Work, and Energy
Unit Themes and Emphases
- Energy, Equilibrium and Systems
- Nature of Science
- Scientific Inquiry
Focusing Questions
- What is necessary to maintain circular motion?
- How does an understanding of conservation laws contribute to an understanding of the Universe?
- How can mechanical energy by transferred and transformed?
Unit C: Circular Motion, Work and Energy
Themes: Energy and Equilibrium
Overview:
In this unit, students extend their study of kinematics and dynamics to uniform circular motion and to mechanical energy, work and powerThis unit builds on:
- •Grade 8 Science, Unit D: Mechanical Systems
- •Grade 9 Science, Unit E: Space Exploration
- •Science 10, Unit B: Energy Flow in Technological Systems
- •Physics 20, Unit A: Kinematics and Unit B: Dynamics
Unit C will require approximately 30% of the time allotted for Physics 20.
Focusing Questions:
- What conditions are necessary to maintain circular motion?
- How does an understanding of conservation laws contribute to an understanding of the universe?
- How can mechanical energy be transferred and transformed?
General Outcomes:
There are two major outcomes in this unit.Students will:
C1. explain circular motion,using Newton’s laws of motion
C2. explain that work is a transfer of energy and that conservation of energy in an isolated system is a fundamental physical concept
Key Concepts:
The following concepts are developed in this unit and may also be addressed in other units or in other courses. The intended level and scope of treatment is defined by the outcomes.Key Concepts:- uniform circular motion
- planetary and satellite motion
- Kepler’s laws
- mechanical energy
- conservation of mechanical energy
- work-energy theorem
- isolated systems
- power
General Outcome 1
C1. Students will explain circular motion, using Newton’s laws of motion.Specific Outcomes for Knowledge
Students will:
20–C1.1k describe uniform circular motion as a special case of two-dimensional motion 5.1
20–C1.2k explain, qualitatively and quantitatively, that the acceleration in uniform circular motion is directed toward the centre of a circle 5.1
20–C1.3k explain, quantitatively, the relationships among speed, frequency, period and radius for circular motion 5.2
20–C1.4k explain, qualitatively, uniform circular motion in terms of Newton’s laws of motion 5.2
20–C1.5k explain, quantitatively, planetary and natural and artificial satellite motion, using circular motion to approximate elliptical orbits 5.3
20–C1.6k predict the mass of a celestial body from the orbital data of a satellite in uniform circular motion around the celestial body 5.3
20–C1.7k explain, qualitatively, how Kepler’s laws were used in the development of Newton’s law of universal gravitation. 5.3
20–C1.2k explain, qualitatively and quantitatively, that the acceleration in uniform circular motion is directed toward the centre of a circle 5.1
20–C1.3k explain, quantitatively, the relationships among speed, frequency, period and radius for circular motion 5.2
20–C1.4k explain, qualitatively, uniform circular motion in terms of Newton’s laws of motion 5.2
20–C1.5k explain, quantitatively, planetary and natural and artificial satellite motion, using circular motion to approximate elliptical orbits 5.3
20–C1.6k predict the mass of a celestial body from the orbital data of a satellite in uniform circular motion around the celestial body 5.3
20–C1.7k explain, qualitatively, how Kepler’s laws were used in the development of Newton’s law of universal gravitation. 5.3
Specific Outcomes for Science, Technology and Society (STS) (Nature of Science Emphasis)
Students will:
20–C1.1sts explain that the process of scientific investigation includes analyzing the evidence and providing explanations based upon scientific theories and concepts
• examine the role of orbital perturbations in the discovery of outer planets
• examine the evidence for extra-solar planets
20–C1.2sts explain how science and technology are developed to meet societal needs and expand human capability
• explain the functions, applications and societal impacts of geosynchronous satellites
20–C1.3sts explain that the goal of technology is to provide solutions to practical problems
• analyze the principles and applications of circular motion in daily situations
– explain the use of a centrifuge in industry or research
– explain the motion of a car moving with constant speed through a curve
– explain the motion of carnival or playground rides moving in a horizontal plane and/or a vertical plane
– explain the operation of a potter’s wheel.
• examine the role of orbital perturbations in the discovery of outer planets
• examine the evidence for extra-solar planets
20–C1.2sts explain how science and technology are developed to meet societal needs and expand human capability
• explain the functions, applications and societal impacts of geosynchronous satellites
20–C1.3sts explain that the goal of technology is to provide solutions to practical problems
• analyze the principles and applications of circular motion in daily situations
– explain the use of a centrifuge in industry or research
– explain the motion of a car moving with constant speed through a curve
– explain the motion of carnival or playground rides moving in a horizontal plane and/or a vertical plane
– explain the operation of a potter’s wheel.
Specific Outcomes for Skills (Nature of Science Emphasis)
Students will:Initiating and Planning
Students will:
20–C1.1s formulate questions about observed relationships and plan investigations of questions, ideas, problems and issues
• design an experiment to investigate the relationships among orbital speed, orbital radius, acceleration and force in uniform circular motion(IP–NS2) Vc lab, Fc lab
• explore design characteristics of structures that facilitate circular motion;
e.g., How is banking used on a racetrack to make high-speed turns safer? ??????
• design an experiment to investigate the relationships among orbital speed, orbital radius, acceleration and force in uniform circular motion(IP–NS2) Vc lab, Fc lab
• explore design characteristics of structures that facilitate circular motion;
e.g., How is banking used on a racetrack to make high-speed turns safer? ??????
Performing and Recording
Students will:
20–C1.2s conduct investigations into relationships among observable variables and use a broad range of tools and techniques to gather and record data and information
• perform an experiment to investigate the relationships among net force acting on an object in uniform circular motion and the object’s frequency, mass, speed and path radius (PR–NS3)
• perform an experiment to investigate the relationships among net force acting on an object in uniform circular motion and the object’s frequency, mass, speed and path radius (PR–NS3)
Analyzing and Interpreting
Students will:
20–C1.3s analyze data and apply mathematical and conceptual models to develop and assess possible solutions
• organize and interpret experimental data, using prepared graphs or charts (AI–NS1)[ICTC7–4.2]
• construct graphs to show relationships among frequency, mass, speed and path radius
• summarize an analysis of the relationships among frequency, mass, speed and path radius (AI–NS6)
• solve, quantitatively, circular motion problems in both horizontal and vertical planes, using algebraic and/or graphical vector analysis (AI–NS3) [ICT C6–4.1]
• organize and interpret experimental data, using prepared graphs or charts (AI–NS1)[ICTC7–4.2]
• construct graphs to show relationships among frequency, mass, speed and path radius
• summarize an analysis of the relationships among frequency, mass, speed and path radius (AI–NS6)
• solve, quantitatively, circular motion problems in both horizontal and vertical planes, using algebraic and/or graphical vector analysis (AI–NS3) [ICT C6–4.1]
Communication and Teamwork
Students will:
20–C1.4s work collaboratively in a ddressing problems and apply the skills and conventions of science in communicating information and ideas and in assessing results
• select and use appropriate numeric, symbolic, graphical or linguistic modes of representation to communicate findings and conclusions (CT–NS2).
Note: Some of the outcomes are supported by examples. The examples are written in italics and do not form part of the required program but are provided as an illustration of how the outcomes might be developed • select and use appropriate numeric, symbolic, graphical or linguistic modes of representation to communicate findings and conclusions (CT–NS2).
Links to Mathematics
The following mathematics outcomes are related to the content of Unit C but are not considered prerequisites.Concept Mathematics Course, Strand and Specific Outcome
Data Collection and Analysis
Grade 9 Mathematics,Statistics and Probability (Data Analysis),Specific Outcome 3 Measurement and Unit Conversions
Mathematics 10C, Measurement, Specific Outcomes 1 and 2;
Mathematics 10-3, Measurement, Specific Outcome 1;
Mathematics 20-3, Algebra, Specific Outcome 3
Trigonometry
Mathematics 10C, Measurement, Specific Outcome 4;
Mathematics 10-3, Geometry, Specific Outcomes 2 and 4
Rate and Proportions
Mathematics 20-2, Measurement, Specific Outcome 1
Graph Analysis
Mathematics10C, Relations and Functions,Specific Outcomes 1, 4 and 7;
Mathematics 20-3, Statistics,Specific Outcome1
Solving Equations
Grade 9 Mathematics, Number, Specific Outcome 6;
Mathematics 20-1, Algebra and Number, Specific Outcome 6;
Mathematics 30-2, Relations and Functions, Specific Outcome 3
Scale Diagrams
Mathematics 20-2, Measurement,Specific Outcome 2;
Mathematics 20-3, Geometry, Specific Outcome 2
Slope
Mathematics10C, Relations and Functions,Specific Outcome 3 and 5;
Mathematics 20-3, Algebra, Specific Outcome 2
Powers
Mathematics10C, Algebra and Number, Specific Outcome 3
Note: The use of systems of equations, the quadratic formula and trigonometric ratios for angles greater than 90º is not required in this unit
Chapter 6. In An Isolated System, Energy Is Transferred From One Object To Another Whenever Work Is Done
Key Concepts
- Work, mechanical energy, and power
- The Work-energy theorem
- Isolated and non-isolated systems.
- The law of conservation of energy
Learning Outcomes
- Use the law of conservation of energy to explain the behaviors of objects within isolated systems.
- Describe the energy transformations in isolated and non-isolated systems using the work-energy theorem
- Calculate power output.
STS
- Explain that models and theories are used to interpret and explain observations.
- Explain that technology cannot solve all problems
- Express opinions on the support found in Canadian society for science and technology measures that work toward a sustainable society.
6.1 Work and Energy
Work is the transfer of energy that occurs when a force acts over a displacement. It is a scalar quantity measured in joules.F - force, N
d - displacement, m
Potential energy is the energy a body has because of its position or configuration. It is a scalar quantity measured in Joules.
Kinetic energy is the energy a body has because of its motion. It is a scalar quantity measured in Joules.
Energy - the ability to do work
Work – a measure of the energy transferred when a force acts over a given displacement. It is calculated as the product of the magnitude of applied force and the displacement of the object in the direction of that force
Gravitational potential energy – the energy of an object due to its position above the surface of Earth
m - mass, kg
g - acceleration due to gravity = 9.81 m/s2
h - height, m
Reference point – an arbitrarily chosen point from which distances are measured
Elastic potential energy – the energy resulting from an object being altered from its standard shape, without permanent deformation
| Fs = -kx |
→
→
|
k - spring constant, N/m
x - stretch or compression
| Es = | kx2 |
| 2 |
k - spring constant, N/m
x - stretch or compression, m
Kinetic energy – the energy due to the motion of an object
| Ek = | mv2 |
| 2 |
m - mass, kg
v - velocity, m/s
Practice Problems
Page 296 Problem1 youtu.be/AkKnxcTJz34Page 296 Problem2 youtu.be/YI5gYh9L4GY
Page 296 Problem3 youtu.be/-f26A6qUtSI
Page 298 Problem1 youtu.be/A0BvvLnkAAo
Page 298 Problem2 youtu.be/9VnFnpx-NcU
Page 298 Problem3 youtu.be/8v5ZKL-j1ao
Page 301 Problem 1 youtu.be/kVlzY3VE9tc
Page 301 Problem 2 youtu.be/5bXrFewhSbQ
Page 301 Problem 3 youtu.be/2DiU4CA1hEw
Page 301 Problem 4 youtu.be/qVPNn5Si_MQ
Page 301 Problem 5 youtu.be/wZX0YlhUBHc
Page 303 Problem1 youtu.be/4J0kue2y35k
Page 303 Problem2 youtu.be/mJktL2k0mFo
Page 303 Problem3 youtu.be/abDzAPghTX0
Page 304 Problem 1 youtu.be/-en10dbT5Tg
Page 304 Problem 2 youtu.be/ekGhFtW9dXY
Page 304 Problem 3 youtu.be/-en10dbT5Tg
Page 305 Question 7 youtu.be/oJwiMGICdrE
Page 305 Question 8 youtu.be/_oUiwT-KSP0
Page 305 Question 9 youtu.be/1MKg3K5U0YU
Page 305 Question 10 youtu.be/Xlg1Tp18ll0
Page 305 Question 11 youtu.be/ntgnJcqJnIM
6.2 Mechanical Energy
Work done by a net force causes a change in kinetic energy.The work-energy theorem states that the work done on a system is equal to the sum of the changes in the potential and kinetic energies.
Mechanical energy is the sum of the potential and kinetic energies.
Mechanics – the study of kinematics, statics, and dynamics
Mechanical energy – the sum of potential and kinetic energies
Work-energy theorem - the product of the force and distance
Practice Problems
Page 308 Problem 1 youtu.be/zwG_yI_9PzYPage 308 Problem 2 youtu.be/xP3XB-0uGEA
Page 308 Problem 3 youtu.be/COW8joiyZXw
Page 309 Problem 1 youtu.be/F1fbsyvxTz8
Page 309 Problem 2 youtu.be/WAbUQ8dCR7I
Page 309 Problem 3 youtu.be/aE_csi3g2vs
6.3 Mechanical Energy In Isolated and Non-isolated Systems
The law of conservation of energy states that in an isolated system, the mechanical energy is constant.A simple pendulum is a good approximation of an isolated system in which energy is conserved.
A conservative force does not affect the mechanical energy of a system.
In non-isolated systems, the mechanical energy may change due to the action of non-conservative forces.
Isolated system – a group of objects assumed to be isolated from all other objects in the universe
Non-isolated system – a system in which there is an energy exchange with the surroundings
Conservation of energy - the total amount of energy in a conservative system (No outside forces) stays the same.
Practice Problems
Page 313 Problem 1 youtu.be/VeUROKfM9poPage 313 Problem 2 youtu.be/I4kbNnGhwYE
Page 313 Problem 3 https://youtu.be/PVwkMjwx0KQ
Page 315 Problem 1 youtu.be/oa4ACnMwk7w
Page 315 Problem 2 youtu.be/OrZjeMR_VlQ
Page 315 Problem 3 youtu.be/Y6RDiy4jqi0
Page 315 Problem 4 youtu.be/Rire48AJbhU
Page 323 Problem 7 youtu.be/p7Fqg1VzQWA
Page 323 Problem 8 youtu.be/_VkYwFw0osA
Page 323 Problem 9 youtu.be/CvZiL1mSYzo
Page 323 Problem 10 youtu.be/RpxTaT3MfKU
6.4 Work and Power
Power is defied as the rate of ding work. Power is calculated by find the ratio of the work done to the time required to do the work. It is measured in Watts.Power may be calculated by taking the product of the force doing the work and the average speed.
Power – the rate of doing work
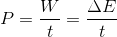
| P = | W |
| t |
W - work or energy, J
t - time, s
A horse power is 746 Watts. Example of half a horse power by a person: www.youtube.com/watch?v=BAutHXpOLBQ
Efficiency – ratio of the energy output to the energy input of any system
| % efficiency = | input energy | × 100% |
| output energy |
input energy - the energy put into the energy conversion, J
output energy - the energy removed from the energy conversion, J

